LCS Tutorial: LCS as Ridges in the FTLE Field

5 LCS as Ridges in the FTLE Field

For time-independent systems, separatices are given by the stable and unstable manifolds of hyperbolic fixed points, as in the pendulum and time-independent double-gyre examples presented thus far. For those examples the separatrices were exposed as ridges in the FTLE field. However, even for highly time-dependent systems, the FTLE fields admit analogous ridges that divide dynamically different regions, but for such systems these structures are themselves time-dependent. Notions such as stable or unstable manifolds are well defined for time-independent flows, but for general time-dependent flows, these notions become ambiguous. However, one can loosely think of studying a time-dependent flow in terms of LCS as the analog of studying a time-independent flow in terms of stable and unstable manifolds. Experience dictates that a wide range of systems admit well-defined ridges in the FTLE fields which govern the global flow structure, however we would like to precisely know: Do LCS represent invariant manifolds?

Before we can answer this question, we must define LCS more precisely. If we refer to LCS as ridges of the FTLE field, we must define a ridge. Intuitively, a ridge is a curve such that if somebody walking along a ridge, then stepping in the direction transverse to the ridge meant that they would be stepping down, and additionally the topography would drop off most steeply in that direction. Or restating, they would be at a local maximum transverse to the curve, and the curvature would be steepest downward transverse to the curve. The definition below makes these ideas precise. First, let us denote the Hessian (second derivative) of $σ$ by $Σ$ , i.e.

2 t0 d---σ-T-(x)--- Σ = . dx2

(15)

We write $Σ$ without explicit reference to its functional dependencies to avoid notational clutter.

Definition 5.1 A ridge of $σ$ is an injective curve $c : s ↦→ D$ , where $s ∈ (a, b) ⊂ ℝ$ , satisfying the following conditions for each s in the open interval (a, b):

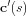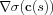SR1: The vectors $c ′(s)$ and $∇ σ(c(s))$ are parallel.
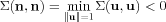
SR2: $Σ(n, n) = min Σ(u, u) < 0 ∥u ∥=1$

where n is a unit normal vector to the curve c(s) , and $Σ$ is thought of as a bilinear form evaluated at the point c(s).

As an aside, a more geometric and covariant definition of a ridge can be given in terms of principal curvatures. For such a definition, including a comparison with the above definition, please refer to the attachment here.

Since the FTLE field, $σT (x) t$ , varies with time, t, it is often convenient to append a subscript on c(s) to refer to the time at which the FTLE is computed. Therefore, we write c_t(s) for a ridge in the FTLE field at time t. We would like to show that c_t(s) behaves as invariant manifolds when t is varied.

We can now formally state:

Definition 5.2 At each time t, a Lagrangian Coherent Structure (LCS) is a ridge of the scalar field $T σ t (x)$ .

Since we assumed that the dynamical system is smooth, the FTLE given by (10) is smooth. By SR1, ridges in the FTLE field are given by special gradient curves, hence LCS are smooth curves, since the gradient of the FTLE field is smooth. However, Shadden, et al (2005) considers the less restrictive case where v is $2 C$ in space and $0 C$ in time, assumptions which are more reasonable in the realm of fluid mechanics.

Comments, Questions or Concerns can be sent to shawn@cds.caltech.edu